Definition, equation, and example
Everyone has heard of a bell curve and has a general idea of what it is. Bell curves, regardless of their exact shape, are described by the normal distribution (aka "Gaussian distribution") equation, normalized to the number of individuals in the studied population. The normal distribution is a continuous probability density function (PDF) that is symmetrical around the mean. The normal distribution equation describes the probability of observing a value x, in a population with a mean \(\mu\) and a standard deviation \(\sigma\) (variance = \(\sigma^2\)). The equation is:
$$p(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-1}{2}{(\frac{x-\mu}{\sigma})}^{2}}$$ $$\text{The Normal Distribution Equation}$$
- the mean, median, and mode are all equal in a normal distribution
- the standard deviation (or its square, the variance) is the measure of the spread of the graph
- In a PDF the probability of an observation p(x) is always positive
- In a PDF of all probabilities in a given interval adds up to 1
- For the normal distribution the sum of all probabilities from \(-\infty\) to \(+\infty\) equals 1.
$$\int_{- \infty}^{+\infty}{\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{- 1}{2}{(\frac{x -
\mu}{\sigma})}^{2}}dx = 1\ \ }$$
$$\text{ The Sum of All Probabilities}$$
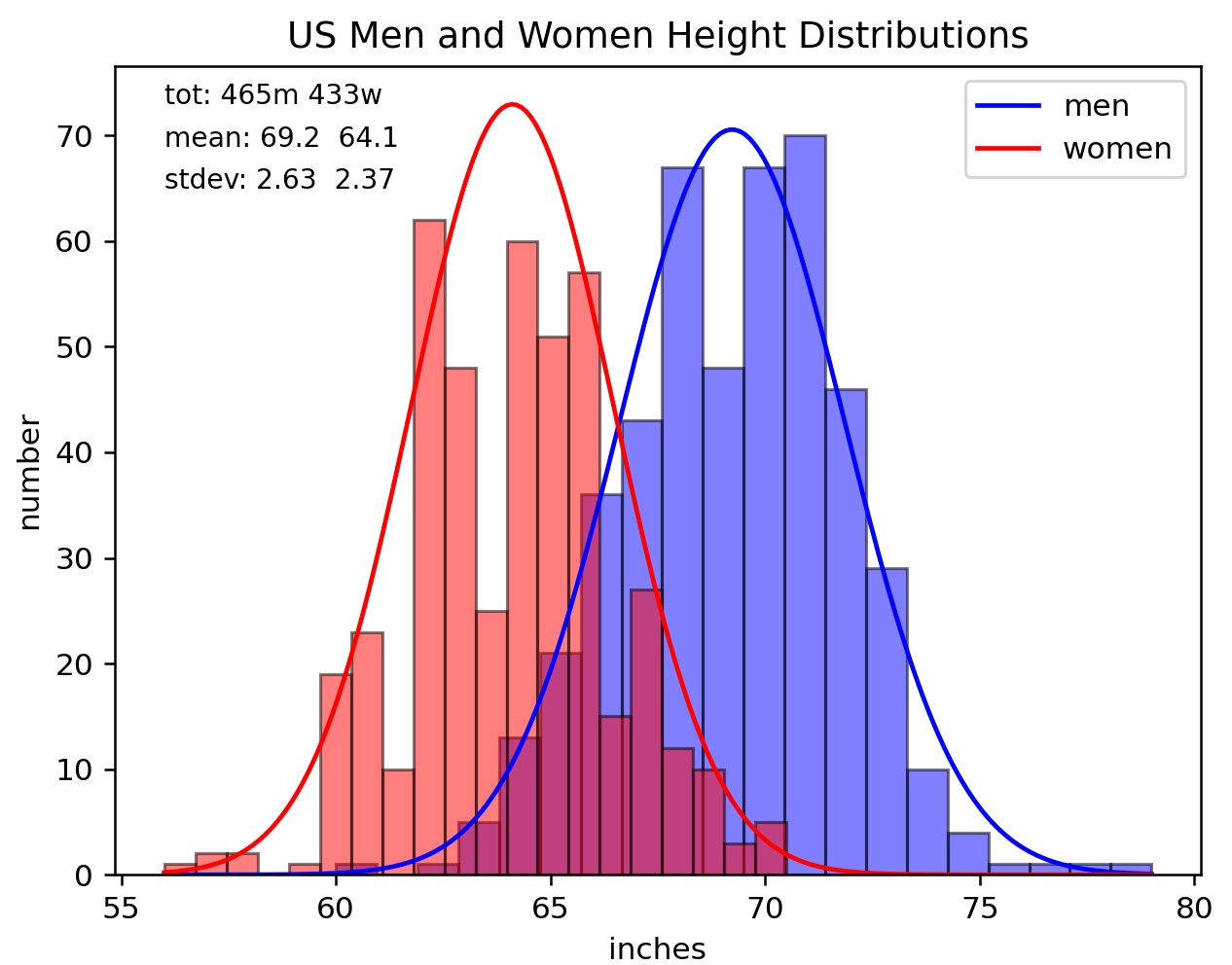
Fig 1 Python Code
import matplotlib.pyplot as pltimport numpy as np
from scipy.stats import norm
dataFile1 = "data_heightMen.txt"
dataFile2 = "data_heightWomen.txt"
nmbrBins = 20
with open(dataFile1, "r") as f1:
data1 = [float(line.strip()) for line in f1]
with open(dataFile2, "r") as f2:
data2 = [float(line.strip()) for line in f2]
[counts1, bins1, patches1] = plt.hist(data1, color="blue", ec="black", alpha=0.5, bins=nmbrBins)
[counts2, bins2, patches2] = plt.hist(data2, color="red", ec="black", alpha=0.5, bins=nmbrBins)
tot1 = sum(counts1)
tot2 = sum(counts2)
m1, s1 = norm.fit(data1)
m2, s2 = norm.fit(data2)
x1 = min(min(data1), min(data2))
x2 = max(max(data1), max(data2))
x = np.linspace(x1, x2, 200)
y1 = norm.pdf(x, m1, s1) * tot1
y2 = norm.pdf(x, m2, s2) * tot2
plt.plot(x, y1, color="blue", label='men')
plt.plot(x, y2, color="red", label='women')
plt.xlabel('inches')
plt.ylabel('number')
plt.title('US Men and Women Height Distributions')
ypos = max(max(y1), max(y2))
plt.text(x1, ypos, f'tot: {tot1:.0f}m {tot2:.0f}w', fontsize=9, color='black')
plt.text(x1, ypos-4, f'mean: {m1:.1f} {m2:.1f}', fontsize=9, color="black")
plt.text(x1, ypos-8, f'stdev: {s1:.2f} {s2:.2f}', fontsize=9, color="black")
plt.legend()
plt.show()
The histograms in Figure 1 are superimposed with corresponding normal distribution curves. Actually, you can't fit the data to a normal distribution equation because, obviously, the men's and women's sample sizes are greater than one. Since the total area under a normal distribution curve is 1, if we want to fit the histograms to a normal distribution, we need to normalize it to the sample size, which amounts to multiplying the PDF by the respective sample sizes (n).
$$y=n\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{- 1}{2}{(\frac{x-\mu}{\sigma})}^{2}}$$ $$\text{Normalizing to the Sample Size}$$ Once we do that we get the fitted plots shown in Figure 1. Well, we also need to plug \(\mu\) and \(\sigma\) into the PDF equation. If those values are unknown they can be calculated by fitting the PDF to the data, which is actually what we did (see the Python code that generated the figure right after the legend - data not included). Before we look at the definitions of the mean \(\mu\) and variance \(\sigma^2\) (the standard deviation is \(\sigma\) ), we must distinguish between a population and a sample. We usually don't have data for the entire population; rather, we have a sample or samples of the population from which we are trying to estimate, within a defined confidence interval, population parameters such as its mean and standard deviation.
Mean, variance/standard deviation: population and sample formulas
The formulas for the sample mean x̄ and the population mean \(\mu\) are the same. $$\overline{x} = \frac{\sum_{i=1}^{1=n}x_{i}}{n};\ \ \ \mu = \frac{\sum_{i=1}^{1=N}x_{i}}{N}$$ $$\text{Sample versus Population Mean}$$ But, the formulas for the sample variance s2 and population variance \(\sigma^2\) are different, although the calculated values will get closer to each other as the sample size increases.
$$s^2=\frac{\sum_{i=1}^{i=n}{{(x_{i}-\overline{x}\ )}^{2}\ }}{n - 1};\ \ \ \sigma^2 = \frac{\sum_{i=1}^{i=N}{{(x_{i}-\mu)}^{2}}}{N}$$ $$\text{Sample versus Population Variance}$$
The \(\mu\) and the \(\sigma^2\) formulas for the theoretical normal distribution PDF are:
$$\mu=\int_{-\infty}^{+\infty}{xp(x)dx}; \ \ \ \sigma^2=\int_{-\infty}^{+\infty}{(x-\mu)^2p(x)dx}$$
$$\text{Mean and Variance Expressed as Integrals}$$
The following example might help understand the correspondence between the integral and the summation formulas.
Suppose we have a histogram with just five bins for heights in inches : 60", 65", 70", 75", 80", where the 60" bin
accommodates people with heights 57.5" to 62.5", the next bin for 62.5" to 67.5", and so on, and that the
numbers of people in those bins are, respectively 3, 10, 30, 12, 5. What is the mean height?
Since the total number of people is 60. The mean is (3/60)x60" + (10/60)x65" + (30/60)x70" + (12/60)x75" + (5/60)x80" = 70.5".
This calculation corresponds to the integral formula, where each term is p(x)dx. The summation formula further up
is exactly the same calculation written as (3x60" + 10x65" + 30x70" + 12x75" + 5x80")/60 = 70.5".
Yet another way to define the mean and variance is by using the expected value operator \(\mathbb{E}\).
$$\mu=\mathbb{E}[x]; \ \ \ \sigma^2 = \ Var(X) = \ \mathbb{E}[X-\mathbb{E}[X]^2]$$
$$\text{Mean and Variance Defined by the Expected Value Operator}$$
Derivation of the normal distribution equation
Next let's derive the normal distribution equation so that it is not a "black box". Although this is a long derivation, you should be able to follow it you have a basic understanding of calculus. I took the derivation from this web page The normal distribution: A derivation from basic principles, by Dan Teage, but will explain in more detail some of the steps that might not be obvious to non-mathematicians like me. Click on the arrow below to see the derivation.
Derivation of the equation for the normal distribution
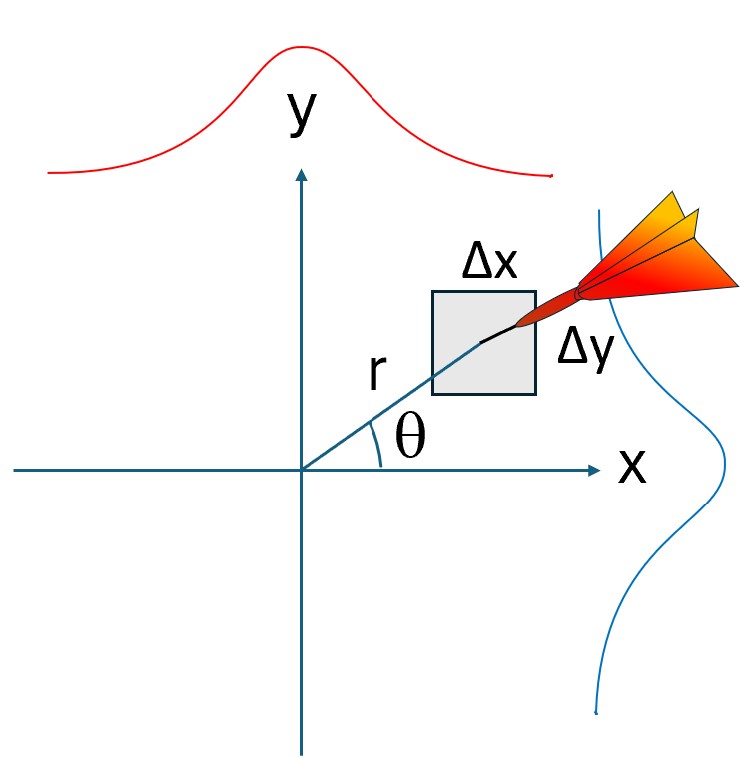
Imagine throwing darts aiming at a point (0,0) on a 2D surface. The probability of it hitting a region with area \(\Delta\)x\(\Delta\)y, at distance r from the origin fits the normal distribution equation because:
- it is a positive number
- it is independent of the angle \(\theta\)
- it is proportional to the area of the square \(\Delta\)x\(\Delta\)y, and
- it decreases as r increases.
- Also, the sum of all probabilities is exactly 1 (or 100%) by definition.
The derivation starts with the formulation of a simple equation that describes the above criteria. $$f(x)\Delta xf(y)\Delta y = g(r)\Delta x\Delta y$$ The right side of the equation exactly describes the criteria. The left side of the equation is less obvious to me. Here is how I rationalize it: hitting the area around (x,y) = (1,1) is more probable than hitting (x,y) = (1,10), which is what we get if we multiply the two probabilities f(x)f(y). Another way to justify it, is by taking all the points that a dart hits and projecting them either along the x-axis or the y-axis. The density of the projected points along either of the axis, f(x) or f(y), should follow a normal distribution because it obeys the above listed criteria. That is f(x) and f(y) are both normal distributions with the same \(\mu\) and \(\sigma^2\) parameters. Figure 2 illustrates this, where the blue and red curves are the normal distributions for x and y, respectively.
The above equation simplifies to: $$f(x)f(y)=g(r)$$ Since the probability is independent of \(\theta\), we can write: $$\frac{d[f(x)f(y)]}{d\theta} = 0$$ $$\text{Expand and substitute in} \ x = rcos(\theta) \ and \ y = rsin(\theta).$$ $$f^{'}(x)\frac{drcos(\theta)}{d\theta}f(y) + f(x)f^{'}(y)\frac{drsin(\theta)}{d\theta} = $$ $$f^{'}(x)(-rsin(\theta))f(y) + f(x)f^{'}(y)rcos(\theta) = 0$$ $$xf(x)f^{'}(y) = f^{'}(x)yf(y)$$ $$\frac{f^{'}(y)}{yf(y)} = \frac{f^{'}(x)}{xf(x)}$$ If two expressions are equal for any x and y, (the key word here is "any") it implies that they are equal to some constant value. So, let us solve one of these differential equations (the other will be solved in the same way): $$\frac{f^{'}(y)}{yf(y)} = k \rightarrow \frac{f^{'}(y)}{f(y)} = ky \rightarrow \int \frac{f^{'}(y)}{f(y)}dy = \int kydy$$ $$ln(f(y)) = k\frac{1}{2}y^2+C\rightarrow f(y) = e^{k\frac{1}{2}{y^2}+C}= e^{C}e^{k\frac{1}{2}{y^2}} = Ae^{\frac{ky^2}{2}}$$ f(x) is the same and it is the basic form of the normal distribution equation. $$f(x) = Ae^{\frac{kx^{2}}{2}}$$ By the above criteria the integral of f(x) from \(-\infty\) to \(+\infty\) is 1. This means that k must be negative, because otherwise the integral would be infinite. Next, rewrite k as -m and figure out what A and m are. We will need to use a couple of mathematical tricks. First, let us look at the figure again and realize two things: (a) the means for both f(x) and f(y) are 0, and both the curves are symmetrical around the mean. Therefore, if we restrict ourselves to the first quadrant (x and y both 0 or positive), the integral of each function will be 1/2. In polar coordinates the positive x and y spaces correspond to 0 to \(\pi\)/2. Now, let us multiply the integral of f(x) by the integral of f(y) in the first quadrant: $$A^2\int_{0}^{\infty}e^{\frac{-m}{2}x^2}dx \int_{0}^{\infty}e^{\frac{-m}{2}y^2}dy = (\frac{1}{2})(\frac{1}{2}) = \frac{1}{4}$$ Now comes the first math trick: we can write the product of the two integrals as a double integral and combine their respective expressions. Fubini's theorem makes this possible. $$A^2\int_{0}^{\infty}\int_{0}^{\infty}e^{\frac{-m}{2}(x+y)^2}dxdy = \frac{1}{4}$$ The second trick is to convert the double integral to polar coordinates. $$A^2\int_{0}^{\frac{\pi}{2}}\int_{0}^{\infty}e^{\frac{-m}{2}r^2}rdrd\theta = \frac{1}{4}$$ To do the cartesian-polar transformation we need to calculate its Jacobian determinant (Jacobian).
$$x = rcos(\theta) \ and \ y = rsin(\theta)$$ $$\frac{dx}{dr}=cos(\theta),\frac{dy}{dr}=sin(\theta),\frac{dx}{d\theta}=-rsin(\theta),\frac{dy}{d\theta}=rcos(\theta)$$
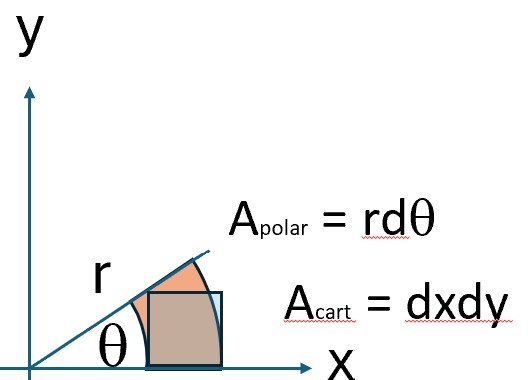
$$The \ Jacobian \ of \ \frac{d(x,y)}{d(r,\theta)} = \begin{vmatrix} \frac{dx}{dr} & \frac{dx}{d\theta} \\ \frac{dy}{dr} & \frac{dy}{d\theta} \end{vmatrix} = \begin{vmatrix} cos(\theta) & -rsin(\theta) \\ sin(\theta) & rcos(\theta) \end{vmatrix}$$ $$cos(\theta)rcos(\theta)-sin(\theta)(-rsin(\theta)) = r(cos(\theta)^2+sin(\theta)^2) = r$$
So dxdy transform to rdrd\(\theta\), because dr must be multiplied by the Jacobian (r) for this transformation. Figure 3 should help you understand this intuitively.
Next, solve the inner integral by using "integration by substitution". Let U = (1/2)mr2, then du/dr = mr, du/m = rdr, substituting into the integral above: $$\int_{0}^{\frac{\pi}{2}}\int_{0}^{\infty}e^{-U}dUd\theta = \frac{m}{4A^2}$$ $$-\frac{1}{e^\infty} - (-\frac{1}{e^0} ) = 0 + 1 = 1$$ $$ \int_{0}^{\frac{\pi}{2}}d\theta = \frac{m}{4A^2} \rightarrow \frac{\pi}{2} =\frac{m}{4A^2}$$ $$A = \sqrt{\frac{m}{2\pi}}$$ $$f(x)=\sqrt{\frac{m}{2\pi}}e^{-\frac{m}{2}x^2}$$ This is closer the the final form of the normal distribution equation, but we still need to figure out what m is (in terms of the mean and variance). The mean \(\mu\) is zero because of the way we derived the equation (aiming the darts at the origin). The variace \(\sigma^2\) can be determined by plugging in the derived equation into: $$\sigma^2=\int_{-\infty}^{+\infty}{(x-\mu)^2p(x)dx} \rightarrow (\mu=0) \rightarrow \sigma^2=\int_{-\infty}^{+\infty}{x^2p(x)dx}$$ $$\sigma^2=\sqrt{\frac{m}{2\pi}}\int_{-\infty}^{+\infty}{xxe^{-\frac{m}{2}x^2}dx}$$ Now we use another math trick called "integration by parts" $$(uv)' = u'v + uv' \rightarrow uv' = (uv)' - u'v \rightarrow \int uv' = uv - \int u'v$$ $$Let \ v'=e^{-\frac{m}{2}x^2} \ and \ u=x \rightarrow u' = 1 \ and \ v =-\frac{1}{m}e^{-\frac{m}{2}x^2}$$ $$Then \ \ \sqrt{\frac{m}{2\pi}}\int_{-\infty}^{+\infty}{xxe^{-\frac{m}{2}x^2}dx} =$$ $$\sqrt{\frac{m}{2\pi}}(x)(\frac{-1}{m})e^{-\frac{m}{2}x^2} - (\frac{-1}{m})\int_{-\infty}^{+\infty}\sqrt{\frac{m}{2\pi}}e^{-\frac{m}{2}x^2}dx$$ The integral on the right side is 1 because it is the sum of all probabilites of the normal distribution. $$\sigma^2 = \sqrt{\frac{m}{2\pi}}(x)(\frac{-1}{m})e^{-\frac{m}{2}x^2} + (\frac{1}{m})$$ $$\sqrt{\frac{m}{2\pi}}(x)(\frac{-1}{m})e^{-\frac{m}{2}x^2}\Biggr|_{-\infty}^{+\infty} = 0 \ because \ \lim_{x \to +/-\infty}\frac{1}{e^{\frac{m}{2}x^2}} = 0$$ $$\sigma^2 = \frac{1}{m} \rightarrow m = \frac{1}{\sigma^2}$$ $$f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x}{\sigma})^2}$$ Finally we can introduce the mean \(\mu\) into the equation by means of a horizontal shift. $$f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}$$
Proof of the sample variance equation
Why do these formulas differ in the denominator (N versus n-1)?
$$\sigma^2=\frac{\sum(x_i - \mu)^2 }{N} \ \ \ s^2=\frac{\sum(x_i - \bar{x})^2 }{n-1}$$
The variance as defined by the equation on the left is valid only if we know
the entire population's mean. However, we usually work with samples, in which case,
we divide by n-1 instead of N.
When writing about the mean and variance we should always use \(\mu\) and \(\sigma^2\)
when referring to a population, and x̄ and s2
when referring to a sample.
The standard way to explain the difference between these two formulas is to say that we lose one
degree of freedom when sampling. Here is why:
suppose I sample 3 of the 4 members of a family whose heights are respectively 3,4,5, and 6 ft.
The true mean is 4.5 ft. But if I sample only 3 members my estimates of the mean are 4, 4.3, 4.7, and 5 ft,
depending on which members I sample (3,4,5) (3,5,6) (3,4,5) or (4,5,6). Now when estimating
the variance, I take the difference between each height and the estimated mean (x̄). Notice however that,
because I already know x̄, after taking two of the numbers, the 3rd number is automatically determined.
That is why we lose one degree of freedom, but it might not so obvious why this leads to
an underestimate of the variance if we use n rather than n-1 in the denominator. This underestimate arises from the smaller spread of the sample
when compared to the real spread of the population, which could be much larger. Therefore, dividing
by n-1 will correct the underestimate by decreasing the denominator.
To make sure let us prove this mathematically.
Proof of the sample variance equation
Proof that \( s^2 \) is an Unbiased Estimator of \( \sigma^2 \)
We wish to show that
$$\mathbb{E}[s^2] = \mathbb{E}\left[\frac{\sum_{i=1}^{n}(X_i-\bar{X})^2}{n-1}\right] = \sigma^2.$$
Note: For simplicity, we write \(\sum X_i\) instead of \(\sum_{i=1}^n X_i\).
Here, \(X\), \(Y\), \(Z\) denote random variables (i.e. processes that generate outcomes before they are observed), and each \(X_i\) is an independent realization of the same random variable \(X\).
The following equalities will be used in the proof:
- \( \mathbb{E}[X] = \mu \)
- \( \mathbb{E}\left[\sum X_i\right] = \sum \mathbb{E}[X_i] \)
- \( \mathbb{E}[cX] = c\,\mathbb{E}[X] \)
- \( \mathbb{E}[XY] = \mathbb{E}[X]\,\mathbb{E}[Y] \) (for independent random variables).
- \( \operatorname{Var}\Bigl(\sum X_i\Bigr) = \sum \operatorname{Var}(X_i) \) (when the \(X_i\) are independent; see proof below).
- \( \operatorname{Var}(X) = \mathbb{E}[(X-\mathbb{E}[X])^2] = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 \) (see proof below).
- \( \mathbb{E}[\bar{X}^2] = \frac{\sigma^2}{n} + \mu^2 \) (see proof below).
Proof of Equality 5: \( \operatorname{Var}(X+Y)=\operatorname{Var}(X)+\operatorname{Var}(Y) \)
Definition: \( \operatorname{Var}(X) = \mathbb{E}[(X-\mathbb{E}[X])^2] \).
Let \( Z = X+Y \). Then,
$$\operatorname{Var}(Z)= \mathbb{E}\Bigl[(X+Y-\mathbb{E}[X+Y])^2\Bigr].$$
Using the linearity of expectation, \( \mathbb{E}[X+Y] = \mathbb{E}[X]+\mathbb{E}[Y] \), so
$$\operatorname{Var}(Z)= \mathbb{E}\Bigl[(X-\mathbb{E}[X] + Y-\mathbb{E}[Y])^2\Bigr].$$
Expanding the square:
$$\operatorname{Var}(Z)= \mathbb{E}\Bigl[(X-\mathbb{E}[X])^2 + 2(X-\mathbb{E}[X])(Y-\mathbb{E}[Y]) + (Y-\mathbb{E}[Y])^2\Bigr].$$
By linearity,
$$\operatorname{Var}(Z)= \operatorname{Var}(X) + 2\,\mathbb{E}[(X-\mathbb{E}[X])(Y-\mathbb{E}[Y])] + \operatorname{Var}(Y).$$
Note that
$$\operatorname{Cov}(X,Y)= \mathbb{E}[(X-\mathbb{E}[X])(Y-\mathbb{E}[Y])],$$
and for independent random variables, \(\operatorname{Cov}(X,Y)=0\). Thus,
$$\operatorname{Var}(X+Y)=\operatorname{Var}(X)+\operatorname{Var}(Y).$$
Note: The covariance can also be written as
$$\operatorname{Cov}(X,Y)=\mathbb{E}[XY]-\mathbb{E}[X]\mathbb{E}[Y].$$
It is straightforward to use algebra and some of the above equalities to show the equivalence between this covariance formula and the one further above. Also,
this covariance formula together with equality 4, makes it clear that if X and Y are independent, then \( cov(X,Y)=0 \)
Proof of Equality 6: \( \operatorname{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 \)
Starting with the definition, \[ \operatorname{Var}(X) = \mathbb{E}\Bigl[(X-\mathbb{E}[X])^2\Bigr] = \mathbb{E}\Bigl[X^2 - 2X\mathbb{E}[X] + (\mathbb{E}[X])^2\Bigr]. \] Using linearity and identity 3, \[ \operatorname{Var}(X) = \mathbb{E}[X^2] - 2\mathbb{E}[X]\mathbb{E}[X] + (\mathbb{E}[X])^2 = \mathbb{E}[X^2] - (\mathbb{E}[X])^2. \]
Proof of Equality 7: \( \mathbb{E}[\bar{X}^2] = \frac{\sigma^2}{n} + \mu^2 \)
We start from the identity: $$\operatorname{Var}(\bar{X}) = \mathbb{E}[\bar{X}^2] - (\mathbb{E}[\bar{X}])^2,$$ and since \(\mathbb{E}[\bar{X}] = \mu\), we have $$\mathbb{E}[\bar{X}^2] = \operatorname{Var}(\bar{X}) + \mu^2.$$ To show \(\operatorname{Var}(\bar{X}) = \frac{\sigma^2}{n}\), note that \[ \bar{X} = \frac{1}{n}\sum_{i=1}^n X_i. \] By the properties of variance (see Equality 5), \[ \operatorname{Var}(\bar{X}) = \frac{1}{n^2} \operatorname{Var}\Bigl(\sum_{i=1}^n X_i\Bigr) = \frac{1}{n^2}\sum_{i=1}^n \operatorname{Var}(X_i) = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n}. \] The previous step may not be obvious, here are the details: $$Var(\bar{X}) = Var(\frac{1}{n} \sum X_i)=\mathbb{E}[(\frac{1}{n}\sum{X_i}-\mathbb{E}[\frac{1}{n}\sum{X_i}])^2] = $$ $$\mathbb{E}[\frac{1}{n^2} (\sum{X_i})^2 - \frac{2}{n^2}(\sum{X_i})(\mathbb{E}[\sum{X_i}]) + \frac{1}{n^2} (\mathbb{E}[{\sum X_i}])^2]= $$ $$\frac{1}{n^2} \mathbb{E}[(\sum{X_i})^2-2(\sum{X_i})(\mathbb{E}[\sum{X_i}]) + (\mathbb{E}[\sum{X_i}])^2]=$$ $$\text{use equality 3 and liniarity:} \ \mathbb{E}[cX]=c\mathbb{E}[X]$$ $$\frac{1}{n^2}(\mathbb{E}[(\sum{X_i})^2]-2\mathbb{E}[(\mathbb{E}([\sum{X_i}]^2)]) + \mathbb{E}[(\mathbb{E}[\sum{X_i}])^2]])=$$ $$\text{simplify and use equality 6:}$$ $$\frac{1}{n^2}(\mathbb{E}[(\sum{X_i})^2]-(\mathbb{E}[\sum{X_i}])^2) = \frac{1}{n^2} Var(\sum{X_i})=$$ $$\frac{1}{n^2}\sum{\sigma^2}=\frac{1}{n^2} n\sigma^2 = \frac{\sigma^2}{n} $$ Hence, \[ \mathbb{E}[\bar{X}^2] = \frac{\sigma^2}{n} + \mu^2. \]
Now we are ready to prove that the sample variance is an unbiased estimator of the population variance. \[ \sum{(X_i-\bar{X})^2}=\sum{X_i^2}-2\bar{X}\sum{X_i}+\sum{\bar{X}^2}= \] \[ \sum{X_i^2}-2n\bar{X}^2+n\bar{X}^2=\sum{X_i^2}-n\bar{X}^2 \] Therefore, \[ \mathbb{E}[s^2] = \frac{1}{n-1}\left(\sum_{i=1}^{n}\mathbb{E}[X_i^2] - n\,\mathbb{E}[\bar{X}^2]\right). \] Using Equality 6, we have \[ \mathbb{E}[X_i^2] = \sigma^2 + \mu^2, \] and from Equality 7, \[ \mathbb{E}[\bar{X}^2] = \frac{\sigma^2}{n} + \mu^2. \] Thus, \[ \mathbb{E}[s^2] = \frac{1}{n-1}\left(n(\sigma^2+\mu^2) - n\left(\frac{\sigma^2}{n}+\mu^2\right)\right) = \frac{1}{n-1}\left(n\sigma^2+n\mu^2 - \sigma^2 - n\mu^2\right) = \frac{1}{n-1}\left((n-1)\sigma^2\right) = \sigma^2. \] This completes the proof.
Confidence intervals
The probability of a random observation falling within an interval \( x_1 \rightarrow x_2 \) is called a confidence interval. For the normal distribution it is equal to the area under the curve, or the integral: $$\int_{x_1}^{x_2}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left( \frac{x-\mu}{\sigma}\right)^2}dx$$ $$\text{Confidence Interval}$$ This is a non-elementary integral, but approximated numerical solutions can be obtained by using power series methods. Before computers, people used tables of pre-calculated confidence intervals. These tables are still used today because for many people they are simpler to understand than computer programs. Typically, these tables (e.g., https://z-table.com/) give you the cumulative confidence interval, which is calculated using the cumulative distribution function: CDF. Mathematically this is the integral, or the area under curve, from \(-\infty \ to \ x\). Note however that you do not input x, but rather the z-score (z) which you calculate as follows: \(z=\frac{(x-\mu)}\sigma{}\). There is a very good reason to use z-scores rather than x. It is because this way you only a single number z to look up in the table, rather than 3 numbers (\(x, \ \mu, \sigma\)) in all sorts of combinations. Therefore, the CDF is more commonly stated as: $$ \text{CDF}(z) = \Phi(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{z} e^{-\frac{1}{2} t^2} \, dt $$ $$\text{Cumulative Distribution Function (CDF)}$$ Here is a quick derivation of what we just did: $$ \text{Start with the integral of the normal distribution:} \ \frac{1}{\sigma \sqrt{2\pi}} \int_{-\infty}^{x} e^{-\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2} \, dx $$ $$ Substitute \ z = \left( \frac{x - \mu}{\sigma} \right) \Rightarrow \frac{dz}{dx} = \frac{1}{\sigma} \Rightarrow dx = \sigma \, dz $$ $$\text{The upper integral limit} \ x \ becomes \ z = \left( \frac{x - \mu}{\sigma} \right) \text{or simply} \ z$$ $$ \Phi(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{z} e^{-\frac{1}{2} z^2} \, dz $$ But there is a confusing notation in the formula above. The \( z \) value in the upper limit of the integral is a constant corresponding to the \( x \) value that delimits our confidence interval, whereas the \( z \) inside the integral is a variable that can take any real number value \( x \in \mathbb{R} \). Therefore, in order to avoid this confusion, we change the name of the variable inside the integral from \( z \) to \( t \), which, of course, makes no difference mathematically. $$ \Phi(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{z} e^{-\frac{1}{2} t^2} \, dt $$ $$\text{Cumulative Distribution Function (CDF)}$$ As an example, Figure 4 illustrates a distribution with \(\mu\) = 2 and \(\sigma\) = 1. The following are 5 different ways one can ask the same question:
- how likely is it that a random observation will be a number smaller than 3?
- what is the probability that a random observation will yield a number smaller than 3?
- what is the confidence interval for x < 3?
- what is the area under the curve from \(-\infty\) to 3?
- given that the z-value corresponding to 3 is \(\frac{3-2}{1}=1\ ,what \ is \ \Phi(1) \ or \ cdf(1)\)?
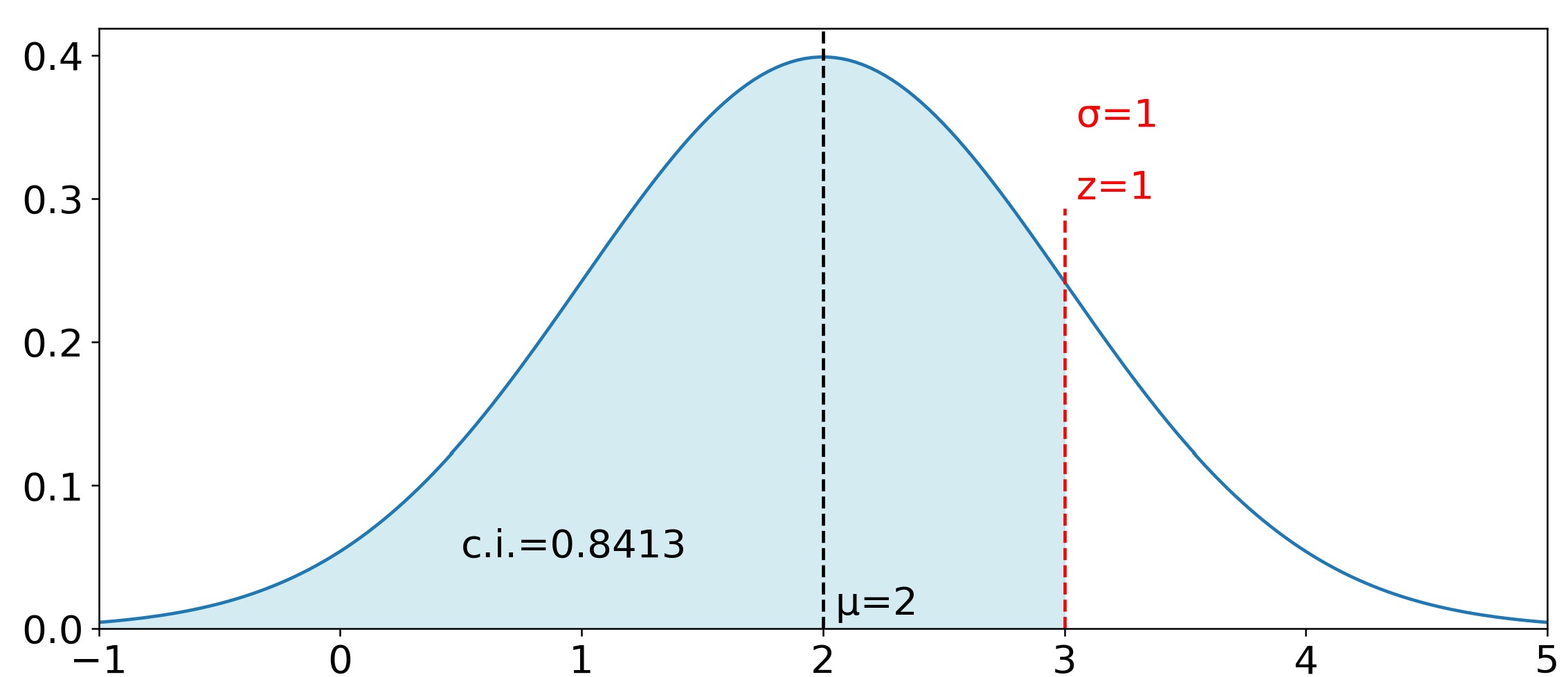
Looking up Z = 1 on the table (https://z-table.com/) you see that the confidence interval cdf is 0.8413. If you prefer using computer programs you can make the same calculation with Python by using the stats.norm.cdf() method. If you click the arrow below you will see the Python code that generated Figure 4. Line 10, ci=stats.norm.cdf(1), defines the variable ci = 0.8413 as the confidence interval for Z = 1.
Fig 4 Python Code
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
m = 2
s = 1
x = np.linspace(-1,5,200)
y = stats.norm.pdf(x,m,s)
x_fill = np.linspace(-1,3,200)
y_fill = stats.norm.pdf(x_fill,m,s)
ci=stats.norm.cdf(1)
fig,ax= plt.subplots(figsize=(12,5))
ax.plot(x,y)
ax.axvline(2,color='black',linestyle='--')
ax.axvline(3,color='red',linestyle='--',ymin=0, ymax=0.7)
ax.tick_params(axis='both',which='major',labelsize=18)
ax.text(2,0.01,' μ=2',fontsize=18, color='black')
ax.text(3,0.35,' σ=1',fontsize=18, color='red')
ax.text(3,0.30,' z=1',fontsize=18, color='red')
ax.text(0.5,0.05,f'c.i.={ci:.4f}',fontsize=18, color='black')
ax.fill_between(x_fill,y_fill,color='lightblue',alpha=0.5)
ax.set_ylim(bottom=0)
ax.set_xlim(left = -1, right = 5)
plt.show()
Now suppose you wanted a 95% confidence interval for the same distribution. You will find that the closest numbers to 0.95 on the table are 0.9495 and 0.9505, corresponding respectively to Z = 1.64 and Z = 1.65. Take 1.64. Thus, a 95% confidence interval corresponds to x < \(\mu\) + 1.64\(\sigma\) → x < 2 + 1.64\(\sigma\) → x < 3.64.
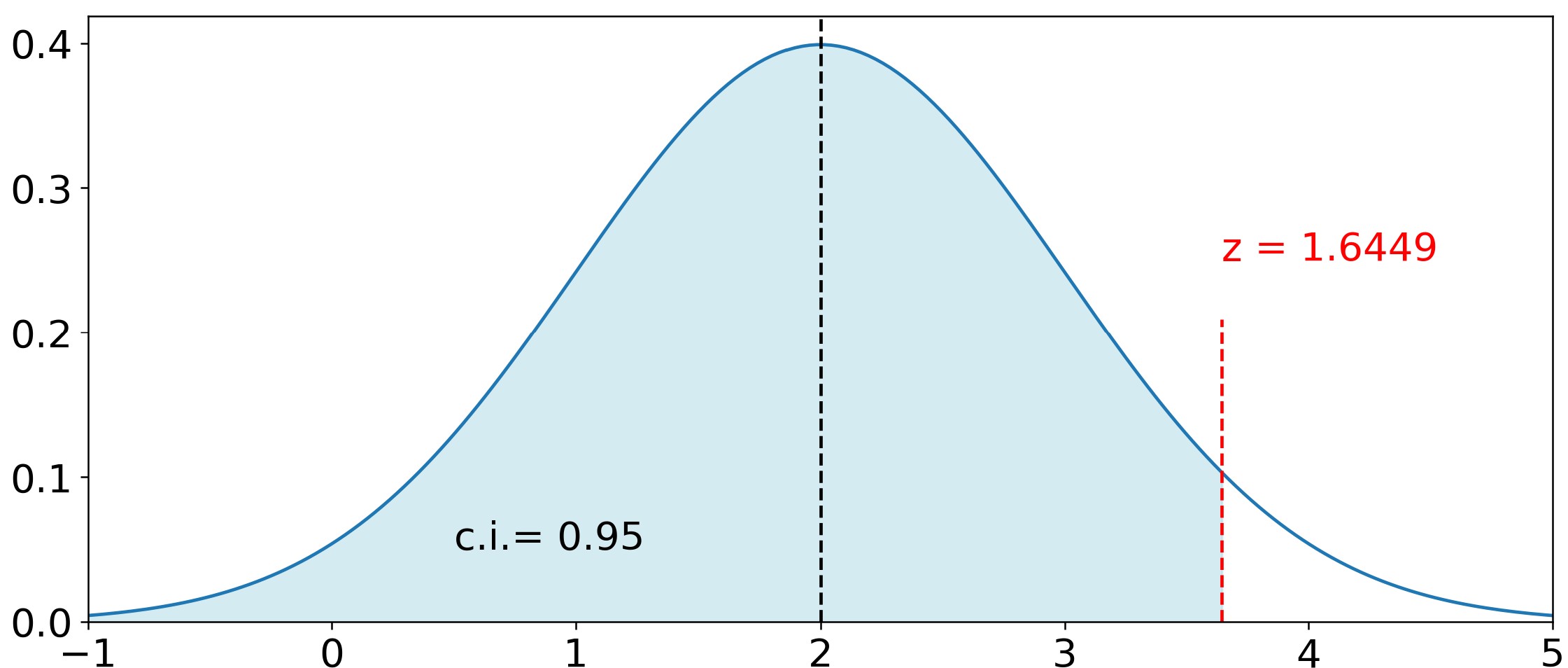
Again, if you click the arrow below you will see the Python code that generated Figure 5. Line 8, z = stats.norm.ppf(0.95), defines the variable z = 1.6449 as the Z value corresponding to a 95% confidence interval.
Fig 5 Python Code
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
m = 2
s = 1
x = np.linspace(-1, 5, 200)
y = stats.norm.pdf(x, m, s)
z = stats.norm.ppf(0.95)
x_fill = np.linspace(-1, m + z * s, 200)
y_fill = stats.norm.pdf(x_fill, m, s)
fig,ax= plt.subplots(figsize=(12,5))
ax.plot(x, y)
ax.axvline(m, color='black', linestyle='--')
ax.axvline(z * s + m, color='red', ymin = 0, ymax = 0.5, linestyle='--')
ax.tick_params(axis='both', which='major', labelsize=18)
ax.text(z * s + m, 0.25, f'z = {z:.4f}', color='red', fontsize=18)
ax.text(0.5, 0.05, f'c.i.= 0.95', fontsize=18, color='black')
ax.set_xlim(left=-1, right=5)
ax.set_ylim(bottom=0)
ax.fill_between(x_fill, y_fill, color='lightblue', alpha=0.5)
plt.show()
Sometimes we want a two-tailed confidence interval (ci) for observations that fall equally to the right and to the left of the mean. For a 95% ci, this means we need to find the Z value corresponding to 97.5% since 2.5% of the remaining area under the curve is on each of the tail ends. Figure 6 illustrates how to do this calculation and compares the one-tail and two-tail ci possibilities.
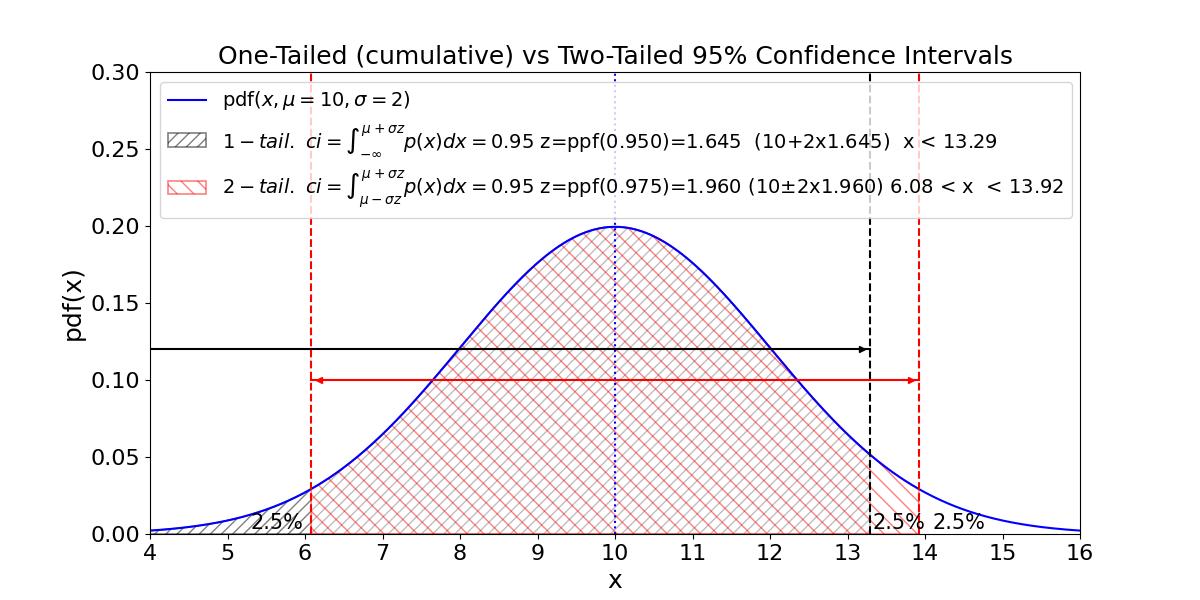
Fig 6 Python Code
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# GLOBAL VARIABLES
adjst = 0.1 # Adjust arrow heads position
m = 10
s = 2
z_ctr = stats.norm.ppf(0.975) # 95% CI (2-tailed)
z_cml = stats.norm.ppf(0.950) # 95% CI (1-tailed cumulative)
x1 = m - z_ctr * s
x2 = m + z_ctr * s
x3 = m + z_cml * s
x_ = np.linspace(m - 3 * s, m + 3 * s, 1000)
y_ = stats.norm.pdf(x_, m, s)
xh_cml = np.linspace(m - 3 * s, x3, 200)
yh_cml = np.full_like(xh_cml, 0.12)
xh_ctr = np.linspace(x1, x2, 200)
yh_ctr = np.full_like(xh_ctr, 0.1)
x_fill_cml = np.linspace(m - 3 * s, x3, 200)
y_fill_cml = stats.norm.pdf(x_fill_cml, m, s)
x_fill_ctr = np.linspace(x1, x2, 1000)
y_fill_ctr = stats.norm.pdf(x_fill_ctr, m, s)
# PLOTS
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(x_, y_, label=r"pdf$(x,\mu=10,\sigma=2)$", color='blue')
ax.axvline(x1, color='red', linestyle='--')
ax.axvline(x2, color='red', linestyle='--')
ax.axvline(x3, color='black', linestyle='--')
ax.axvline(m, color='blue', linestyle=':')
ax.plot(xh_cml, yh_cml, color='black')
ax.plot(x3 - adjst, 0.12, marker='>', markersize=5, color='black')
ax.plot(x1 + adjst, 0.1, marker='<', markersize=5, color='red')
ax.plot(x2 - adjst, 0.1, marker='>', markersize=5, color='red')
ax.plot(xh_ctr, yh_ctr, color='red')
ax.fill_between(x_fill_cml, y_fill_cml, hatch='///', alpha=0.5,
facecolor='white', edgecolor='black', linewidth=1.2,
label=r'$1-tail. \ ci=\int_{-\infty}^{\mu+\sigma z}p(x)dx=0.95$' + f' z=ppf(0.950)={z_cml:.3f} ({m}+{s}x{z_cml:.3f}) x < {x3:.2f}')
ax.fill_between(x_fill_ctr, y_fill_ctr, hatch='\\\\', alpha=0.5,
facecolor='white', edgecolor='red', linewidth=1.2,
label=r'$2-tail. \ ci=\int_{\mu-\sigma z}^{\mu+\sigma z}p(x)dx=0.95$' + f' z=ppf(0.975)={z_ctr:.3f} ({m}'+r'$\pm$'+f'{s}x{z_ctr:.3f}) {x1:.2f} < x < {x2:.2f}')
# AXES AND GRID
ax.set_ylim(bottom=0, top=0.3)
ax.set_xlim(left=m - 3 * s, right=m + 3 * s)
# TITLE, LABELS, AND ANNOTATIONS
ax.set_title('One-Tailed (cumulative) vs Two-Tailed 95% Confidence Intervals', fontsize=18)
ax.set_xlabel('x', fontsize=18)
ax.set_xticks(range(4,17))
ax.set_ylabel('pdf(x)', fontsize=18)
ax.tick_params(axis='both', which='major', labelsize=16)
# Manually adjust text positions
ax.text(5.3, 0.003, '2.5%', fontsize=15, color='black')
ax.text(x3 + 0.03, 0.003, '2.5%', fontsize=15, color='black')
ax.text(14.1, 0.003, '2.5%', fontsize=15, color='black')
ax.legend(loc="upper left", fontsize=14)
# Show plot
plt.show()
The The Gauss Error Function \(\operatorname{erf}(x)\) is found in Excel, Google Sheets, Python, and on many scientific calculators. However, be very careful if you decide to use it because it is not the same as the cumulative density function (CDF). $$\operatorname{erf}(z) = \frac{2}{\sqrt{\pi}}\int_0^z e^{-t^2} dt, \quad \Phi(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{z} e^{-\frac{1}{2} t^2} dt$$ $$\text{ERF(z) versus CDF(z)}$$ The two functions are related as follows: $$\Phi(y) = \frac{1}{2} \left(1 + \operatorname{erf} \left(\frac{y}{\sqrt{2}}\right) \right)$$ $$\text{Relation Between CDF(z) and ERF(z)}$$
Using the Python cdf function (for the normal distribution): ci = stats.norm.cdf(1) yields ci=0.8413447460685429
Using the Excel erf function: =0.5*(1+ERF(1/SQRT(2))) results in: 0.841344746
Proof of the relationship between CDF and ERF
We are going to use the following identities in this proof:
- \(\operatorname{erf}(z) = \frac{2}{\sqrt{\pi}}\int_0^z e^{-t^2} dt\)
- \(\Phi(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{z} e^{-\frac{1}{2} t^2} dt\)
- \(\int_{-\infty}^{+\infty} e^{-u^2} \, du = \sqrt{\pi}\), proof:
- \(\text{The total area under the curve of the normal distribution is 1:} \quad \int_{-\infty}^{+\infty}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \, dx =1\)
- \(\text{Substituting } u=\frac{x-\mu}{\sqrt{2}\sigma} \Rightarrow dx = \sqrt{2}\sigma \, du\)
- \(\int_{-\infty}^{+\infty}\frac{1}{\sqrt{\pi}}e^{-u^2}du=1 \Rightarrow \int_{-\infty}^{+\infty}e^{-u^2}du =\sqrt{\pi}\)
- \(t = \sqrt{2}y \Rightarrow t^2 = 2y^2 \Rightarrow dt=\sqrt{2}dy\)
- \(\text{Due to the symmetry in Equation 3:} \quad \int_{-\infty}^{0}e^{-u^2}du =\frac{\sqrt{\pi}}{2}\)
Substituting \( t \) in Equation 2 using the equalities in step 4: \[ \Phi(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\frac{x}{\sqrt{2}}} e^{-y^2}\sqrt{2} \, dy = \frac{1}{\sqrt{\pi}} \int_{-\infty}^{\frac{x}{\sqrt{2}}} e^{-y^2} \, dy \] Splitting the integral: \[ \frac{1}{\sqrt{\pi}} \int_{-\infty}^{\frac{x}{\sqrt{2}}} e^{-y^2} \, dy = \frac{1}{\sqrt{\pi}} \left( \int_{-\infty}^{0} e^{-y^2} \, dy + \int_{0}^{\frac{x}{\sqrt{2}}} e^{-y^2} \, dy \right) \] Using equalities 1 and 5: \[ \Phi(x) = \frac{1}{\sqrt{\pi}} \left(\frac{\sqrt{\pi}}{2} + \frac{\sqrt{\pi}}{2} \operatorname{erf} \left(\frac{x}{\sqrt{2}} \right) \right) = \frac{1}{2} \left(1 + \operatorname{erf} \left(\frac{x}{\sqrt{2}} \right) \right) \] End of proof.